
A swap fee in Forex, often called a rollover fee or swap points, represents the interest traders pay for holding a position past the end of the trading day. If traders keep their positions open at the daily rollover point, usually at 00:00 server time or “tomorrow next,” they incur the swap fee. These fees reflect the cost of carrying the trade overnight, affecting the overall cost of trading. Therefore, traders need to consider swap fees to manage costs effectively and maximize profitability in Forex trading.
Introduction
We’ve wondered how brokers calculate swap fees at various points in our careers in the Forex industry. When you look into the trading instrument specifications or trading rules that your broker provides on their website, you’ll usually find that when you roll over your open positions to the next trading day, they will either credit or debit a swap fee will from or to your account—the fee triples when your broker rolls over your positions from Wednesday to Thursday.
Your broker might briefly mention that this fee is based on interest rates. However, the detailed calculation of the SWAP fee is something support managers won’t share with you; only the dealing desk knows that. Today’s article will reveal what the average retail trader can’t see—what happens “behind the scenes.” This is a heads-up that there will be a lot of text. So, let’s dive in. We promise it will be interesting.
How Do Large Financial Institutions (e.g., Liquidity Providers) Calculate Swap Fees?
Once, we looked into the reference materials for one of the trading terminals used for interbank market trading. There, we found the following explanation:
Swap Points
DEFINITION
The Forward rate of exchange of a currency against the USD (in other words, the base currency) is generally quoted not as Outright rates but as margins expressed in points above or below their corresponding spot rates.
CALCULATION
Swap points are the mathematical representation of the interest rate differential between the two currencies for a specific period and a specific spot rate. Swap points are either added to or subtracted from the spot rate, depending on the interest rate of each currency in the pair. The bid side of swap points from deposits for currency one (Cur1) and currency two (Cur2) is calculated by the formula:
Swp12b = Spot12b* ( (1+ Dep2b*n/Basis2)/(1+Dep1a*n/Basis1) – 1)
The ask side of swap points from deposits for currency one and currency two is calculated by the formula:
Swp12a = Spot12a* ( (1+ Dep2a *n/Basis2)/(1+Dep1b*n/Basis1) – 1)
Where:
n days from spot to value date for Cur1Cur2
Basis1 money market year basis for Cur1, either 360 or 365
Basis2 money market year basis for Cur2, either 360 or 365
Dep1a ask side of Cur1 deposit rate
Dep1b bid side of Cur1 deposit rate
Dep2a ask side of Cur2 deposit rate
Dep2b bid side of Cur2 deposit rate
Spot12a ask side of Cur1Cur2 spot cross rate
Spot12b bid side of Cur1Cur2 spot cross rate
Swp12a ask side of Cur1Cur2 cross swap point
Swp12b bid side of Cur1Cur2 cross swap point
These points are referred to as forward points or swap points. A Forward Cross Rate between two currencies, neither of which is the USD, can then be quoted as either forward points or Outright rates. In the former case, forward points are called cross-swap points.
It might look intimidating, but let’s break it down – it’s not as scary as it seems!
Let’s walk you through the calculation of swap fees in forex so that you can better understand where everything comes from and how different parameters fit together and affect the result.
The usual formula for calculating interest is:
E(r) = 1 x (1+r)
For example, a 10% return on, say, 100,000 euros would be:
100,000 * (1 + 10%) = 110,000
If you want to specify the period over which the return is earned, you add the number of days to the formula:
E(r) = 1 x (1 + r x days/period)
For example, a 10% annual return on 100,000 euros over three days would be:
100,000 * (1 + 10% * 3/360) = 100,083.3333
The number 360 is the number of days in a year used in standard financial calculations. It can vary depending on the country. Some use 365, but that’s not important for now. Now, let’s apply what we’ve learned to a currency pair. In this scenario, we deal with two transactions so that interest will accrue on both sides.
Let’s say the euro exchange rate is 1.1800, and the euro (r1) interest rate is 0.10%, while the interest rate on the dollar (r2) is 0.25%. This means the return on the euro would be 100,000 * (1 + r1), and the return on the dollar, converted at the exchange rate of 1.18, would be 118,000 * (1 + r2). This results in a certain amount of euros and a certain amount of dollars. If we divide these resulting values, we get an artificial forward rate, taking into account the interest additions:
118,000 * (1 + r2) / 100,000 * (1 + r1) or
118,000 / 100,000 * (1 + r2) / (1 + r1) or
Forward Rate = Current Exchange Rate * (1 + r2) / (1 + r1)
Therefore, to calculate the net profit, we need to subtract the current exchange rate from the forward rate:
Forward Profit = Current Exchange Rate * ((1 + r2) / (1 + r1) – Current Exchange Rate
If we simplify the expression and factor out the “Current Exchange Rate,” the formula transforms into this:
Forward Profit = Current Exchange Rate * ((1 + r2) / (1 + r1) – 1)
If the calculation seeks the return on interest rates r1 and r2 for a certain number of days n out of a year N, then we get:
Forward Profit = Current Exchange Rate * ((1 + r2 * n/N) / (1 + r1 * n/N) – 1)
And this is the averaged formula:
Swp12bid = Spot12b * ((1 + Dep2b * n/Basis2) / (1 + Dep1a * n/Basis1) – 1)
Swp12aask = Spot12a * ((1 + Dep2a * n/Basis2) / (1 + Dep1b * n/Basis1) – 1)
We use two formulas: one is for long positions, and the other is for short ones.
Spot12b and Spot12a are the exchange rates for these positions.
According to the Tom-Next accrual logic, n/Basis2 and n/Basis1 are for 3 out of 360 days. Since the number of days is the same for both currencies, we can replace these parameters with a constant:
Swp12bid = Spot12b * ((1 + Dep2b * 3/360) / (1 + Dep1a * 3/360) – 1)
Swp12ask = Spot12a * ((1 + Dep2a * 3/360) / (1 + Dep1b * 3/360) – 1)
Dep2b and Dep2a are the interest rates for one currency.
Dep1b and Dep1a are the interest rates for the second currency.
In a long position, they will give Swp12a; in a short position, they will receive Swp12b.
In other words, in a long position with a simple Tom-Next (TN) order closure, the client will “pay” a swap fee, while in a short position, they will “receive” a swap fee. This means that if you run a long position, the broker will deduct swap points, while in case of a short position, they will add them to your net financial result.
If the trader reopens the trade, they pay the spread and the swap points. Therefore, in a long position, the trader loses the spread and “pays” the forex swap fee, while in a short position, they lose the spread but receive the swap fee. The value of swap points depends on the currency pair’s price and changes in interest rates, so they can both increase and decrease.
As a result, swap fees are traded as a separate instrument. The client doesn’t need to open an order for 100,000 units of the underlying asset; they can buy or sell the swap directly. Since supply and demand forces determine them, market swap fees can differ significantly from calculated ones.
In a trading terminal, this typically looks like this:
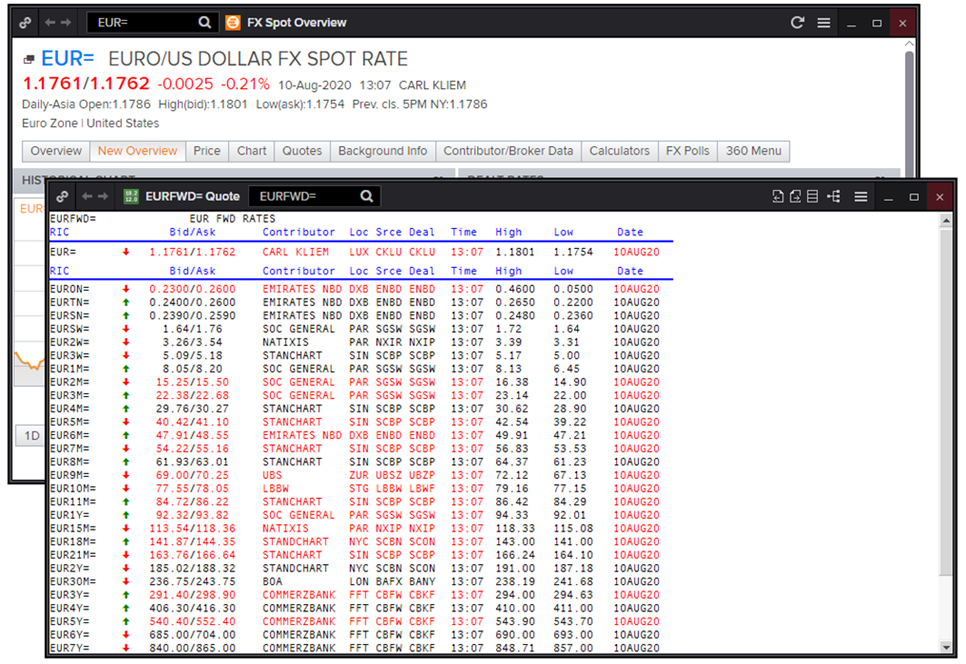
Based on the figure, the exchange rate was 1.1761 / 1.1762
Spread = 0.0001
Therefore, the rollover losses would be: long = -0.0001 – 0.000057 = -0.000157 and
Short = -0.0001 + 0.000054 = -0.000046
Now, let’s look at the same situation with retail forex brokers. In MT4, positions cannot be re-opened, so spread points are added to swap fees, thus magnifying the trader’s expenses.
The data shown above, in MT4, with the addition of spread losses, would look like this:
Swap long = -1.57 and Swap short = -0.46
However, please note that these points are not the result of the calculation. They are the result of supply and demand forces.
And these can differ significantly between different brokers at the same time. For example, with one of the brokers, it looked like this:
Swap long = -3.47 and Swap short = 1.45
This can only happen if a broker adds a particular markup to the interest rate values for each instrument. And they don’t usually disclose their calculation methodology.
If we take the averaged formula for calculating forex swap points, we get the following entity:
Swp = (Ask + Bid) / 2 * ((1 + 0.25% * 3/360) / (1 + 0% * 3/360) – 1)
Swp = (1.1761 + 1.1762) / 2 * ((1 + 0.25% * 3/360) / (1 + 0% * 3/360) – 1) = 0.0000245
where
USD rate = 0.25% and EUR rate = 0% are the interest rates for the currencies,
SWP = 0.0000245 is 0.245 four-digit points
The screenshot above shows that the swap points are 0.24 and 0.26. In this case, the calculated values were very close to the market values. However, such coincidences are rare due to the different liquidity of pairs and the fragmentation of the forex market (i.e., other brokers may have different liquidity providers).
There’s a more straightforward way to calculate swap values, and some brokers use it:
- They fix the spread for the pair as a constant.
- They take the Tom-Next (TN) swap point values from the interbank market.
They then calculate their own swap:
Swap long = – spread – SwapPointsTN_Ask
Swap short = – spread + SwapPointsTN_Bid
This approach results in the most competitive swaps. However, if a broker wants to earn a little more profit, they can further “worsen” the swaps in MT4. By the way, Oanda doesn’t bother with calculations and boldly charges its own interest on each side; consequently, their swaps fees are negative in both directions.
On the other hand, if you are a bank employee working in a dealing department or for a different sell-side financial institution, don’t rush to criticize this text. Your employer might have a different methodology for calculating swaps, of which we are unaware. Therefore, feel free to share it in the comments; we and our readers would be grateful.
Meanwhile, if you are a trader, remember there’s no point in arguing, protesting, or complaining to the broker about their forex swap fee calculations. Since each broker may have a unique way of calculating swap values, it’s essential to consider this information.
In our previous articles (Story 12, Story 13), we reviewed different ways to trade the rollover, in case you were wondering if there were any ways to do that.
DISCLAIMER! The contracts for difference (CFDs) we discuss come with high risks, and you could lose all the money you put in. Make sure you understand all the risks involved before you dive in.
Do The Smart Thing. Subscribe!
Get notified about our new articles and insights.



